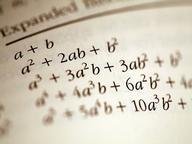Quiz Answer Key and Fun Facts
1. Factor 5(x^3)(y^2)(z) + 100(x^2)(y^3)(z^2) by factoring out their greatest common factor. NOTE: The parentheses have been added to distinguish terms from each other. Factor as normal.
2. Factor the polynomial 4x^2 - 25, using the difference of two perfect squares.
3. Completely factor 2x^2 - 50.
4. Factor the perfect square polynomial 25x^2 + 90x + 81.
5. Factor a^2 + 11a + 24.
6. Factor the trinomial b^2 + 6b - 16.
7. Completely factor 4b^2 + 16b + 16.
8. Factor 3x^2 + 14x + 15.
9. Factor the polynomial 12x^2 + x - 35.
10. To wrap this quiz up, completely factor the following polynomial:
308x^2 + 161x + 21.
Source: Author
XxHarryxX
This quiz was reviewed by FunTrivia editor
crisw before going online.
Any errors found in FunTrivia content are routinely corrected through our feedback system.