Mathematical Names for Objects Quiz
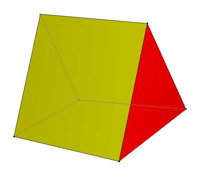
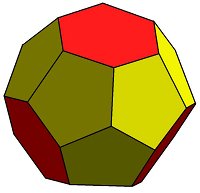
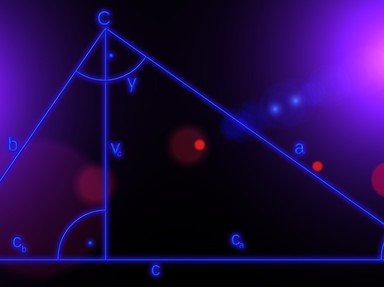
Select the term that a mathematician might use when trying to describe each of the objects shown. Where relevant, these are real life objects, so display imperfections, and are not ideal examples.
by looney_tunes.
Estimated time: 3 mins.
- Home
- »
- Quizzes
- »
- Science Trivia
- »
- Math
- »
- Geometry