Quiz Answer Key and Fun Facts
1. Which plane figure is defined as any polygon with exactly 4 angles, all of whom are equal?
2. Which Solid can be defined as the regular polyhedron (a solid with all faces identical regular polygons) with the greatest number of faces?
3. What shape is created by taking a rectangular sheet of paper, giving it a "twist" and gluing the two ends of the strips together?
4. What solid can be thought of as taking a cylinder, giving it a "twist" in some fourth dimension, and gluing one end of the cylinder to the other end?
5. Of all plane shapes with the same perimeter, which one has the greatest area?
6. What shape can be created by taking a rectangular piece of paper, rolling one pair of opposite sides onto each other (to form a cylinder), then rolling the two opposite circular ends of the cylinder onto each other?
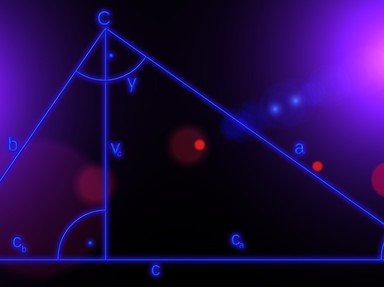
7. If two sides of a triangle are given, what type of triangle containing those two sides will have the greatest area?
8. What Plane Shape can be defined as a quadrilateral whose diagonals bisect each other and are perpendicular?
9. Which of these pairs of shapes CANNOT be used to fill the entire plane (assuming all sides are the same length and some of each shape are used)?
10. Finally, which one of these four solids is not a real shape (i.e. which one did I just make up?)
Source: Author
kevinatilusa
This quiz was reviewed by FunTrivia editor
crisw before going online.
Any errors found in FunTrivia content are routinely corrected through our feedback system.